
Since the base of a logarithm can never be 1, then the only solution is 3. Rewrite the logarithm in exponential form to get Using the product rule Log b (m n) = log b m + log b n we get Write the logarithm in exponential form as įind the square root of both sides of the equation to get īut since, the base of logarithms can never be negative or 1, therefore, the correct answer is 30. Now, solve for x in the algebraic equation. Rewrite the logarithm in exponential form as Solve for x in the following logarithmic function log 2 (x – 1) = 5.

Rewrite the logarithmic function log 2( x) = 4 to exponential form. If 2 log x = 4 log 3, then find the value of ‘x’.įind the logarithm of 1024 to the base 2. Write the logarithmic equivalent of 5 3 = 125. Therefore, 7 2 = 64 in logarithmic function is Here, the base = 7, exponent = 2 and the argument = 49. Rewrite exponential function 7 2 = 49 to its equivalent logarithmic function. Let’s use these properties to solve a couple of problems involving logarithmic functions.
#Derivative of log base 2 x how to
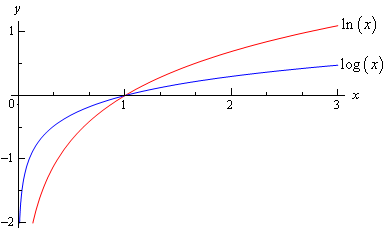
The third column tells about how to read both the logarithmic functions. The following table tells the way of writing and interchanging the exponential functions and logarithmic functions. Both of these functions are interchangeable. For that, you use an exponential function. Whenever you see logarithms in the equation, you always think of how to undo the logarithm to solve the equation. Always assume a base of 10 when solving with logarithmic functions without a small subscript for the base.Ĭomparison of exponential function and logarithmic function A logarithmic function with base 10is called a common logarithm.The base of logarithms can never be negative or 1.
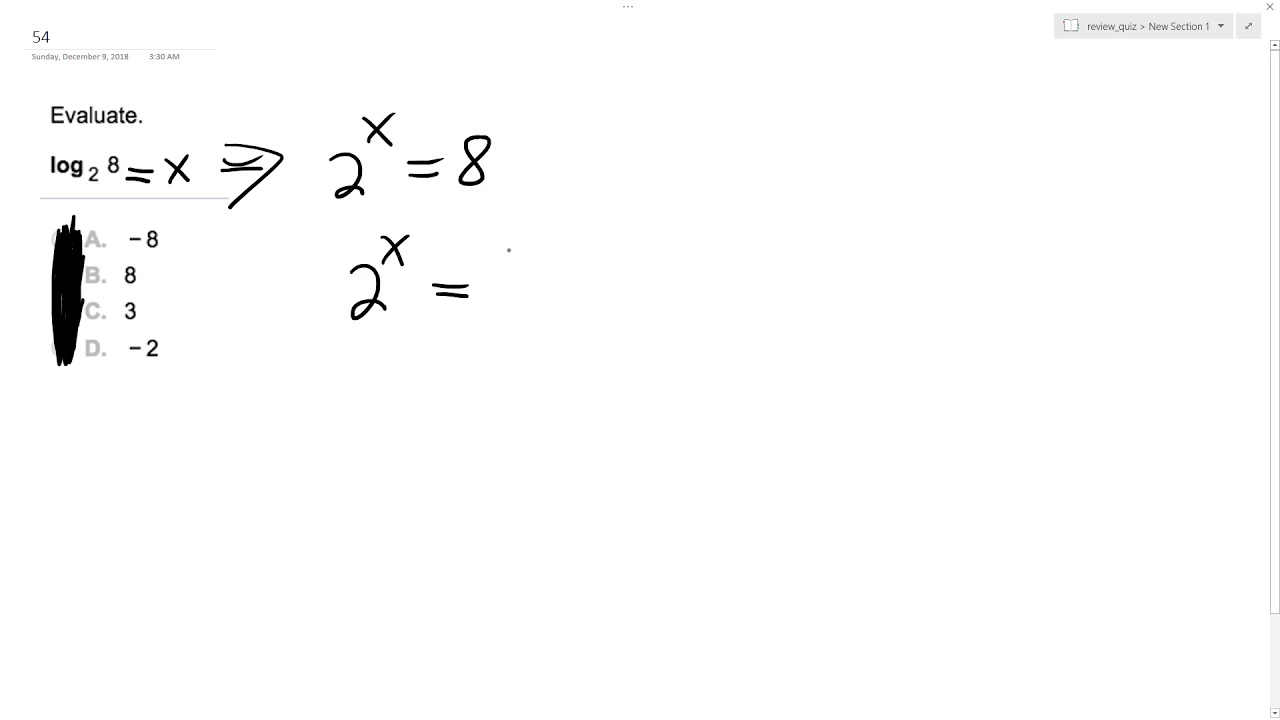
Logarithms and exponents are two topics in mathematics that are closely related. In this article, we will learn how to evaluate and solve logarithmic functions with unknown variables. Solving Logarithmic Functions – Explanation & Examples


 0 kommentar(er)
0 kommentar(er)
